Understanding Biomechanical Engineering Language

Biomechanical engineering describes the properties and the behavior of biological tissues using mechanical engineering principles and terms. Words such as “load”, “force”, “stress”, “strength” and “stiffness” populate marketing materials, white papers, journal articles, and popular media. Bone, cartilage, ligaments, and implants are described using this vocabulary. Unfortunately, these terms are frequently misused and/or misunderstood by both authors and readers. This mini-tutorial on biomechanical engineering will clarify some of the more common language and its engineering definitions.

Structures and Materials

Let’s begin with the difference between “structures” and “materials”. An easy way to remember the distinction is to visualize a building in its early stages of construction. It looks like a huge, complex, erector-set of connected steel beams. The skeletal building is a structure, its properties and behaviors are functions of its geometry, connections, and material. The properties of the material, steel, are dependent on the alloy content and the processing that created it.

Another illustration: the spine. The spine is a structure made of vertebral bodies and intervertebral discs. The vertebrae are also structures in their own right; primarily made of a cortical bone “shell” and a cancellous bone “filling”. To the naked-eye, cortical bone is a material and cancellous bone is a structure. After all, the beam-and-truss “construction” of cancellous bone is easy to see. The small, individual “beams” and “trusses” are the true bone in cancellous bone. On the microscopic level, neither cortical nor cancellous bone are materials, they’re both structures and the individual components, such as calcium phosphate crystals and collagen, are the materials.

Just as the structural properties of the building under-construction are dependent on the alloy and its processing, the structural properties of the spine are dependent on the bone and its health. Osteoporosis affects the strength of bone through the removal of material and the creation of voids. Age affects the strength of intervertebral discs through changes in collagen.

The Basics

The properties of biological tissues are determined by the analysis of structural testing output, often in the form of load versus displacement diagrams [Figure 1]. Each load versus displacement diagram for biological tissues is unique. Not only do the diagrams differ from type of tissue, such as bone and cartilage, they also differ by location, for example the distal radius and the proximal femur. Load versus displacement diagrams also differ with age and health status, the peak load for osteoporotic bone will be less than for healthy, non-osteoporotic bone. This peak load, known as the ultimate load is the point where force and displacement create irretrievable damage to the biological tissue; it is the load where failure occurs (a.k.a. “failure load”).

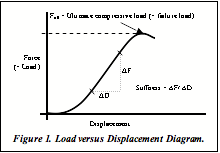
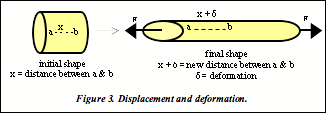
“Load”, also known as “force”, is the external pull or push applied to an object; the units of force are Newtons (N) or pounds (lbs) [Figure 2]. “Displacement” is the difference in the position of a particular point from the initial, unloaded condition to the final, loaded condition. “Deformation” is the relative displacement of any two points in a body. Displacement and deformation have units of length; meters (m), feet (ft), or inches (in) [Figure 3].

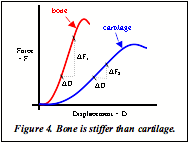
Stiffness is represented by the slope of the straight line on force-displacement diagrams and has units of force per deformation, Newtons per meter (N/m) or pounds per inch (lb/in). Stiffer materials, like bone, are more resistant to deformation at a given load than less stiff materials like cartilage [Figure 4].

Strength, Elasticity, and Viscoelasticity

Although load and strength or stiffness and elasticity are often used interchangeably, they are not the same. Load and stiffness are properties described by force-displacement diagrams while strength and elasticity are properties described by stress versus strain diagrams [Figure 5]. These diagrams are very similar in appearance to load-displacement diagrams, but they represent strength not failure load and elasticity not stiffness.

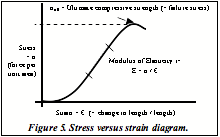
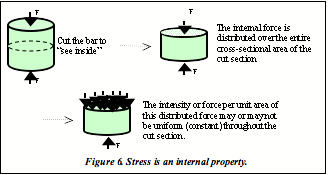
“Stress” refers to the forces within an object. The intensity of the internal force over the cut section is stress and is defined as the force per unit area over which the force is acting [σ = F/A]. Figure 6 illustrates “normal stress”, meaning stress that is perpendicular to the plane of the cut; stress is measured as force per unit area and has units of MPa (N/m2) or psi (lb/in2). “Strength” is analogous to “failure load”, it is a measure of the compressive force at the exact instant of failure.

“Strain” is unit deformation, a measure of the degree or intensity of deformation. Strain is the ratio of change in length (increase or decrease) to original length [є = ∆l/l], and therefore has no units of measure [Figure 7]. When a body is in tension, its length increases and strain is positive. When a body is in compression, its length decreases and strain is negative.

“Elasticity” is defined by Hooke’s Law, E = σ/ є, and is represented by the slope of the straight line on stress-strain diagrams. Elasticity has units of MPa or psi. Within the elastic range, the straight line portion of the stress-strain diagram, deformation is reversible by simply removing the load; for example, a rubber band after being stretched will return to it’s original shape. In the non-linear portion of the stress-strain curve, deformation is plastic and non-reversible; potters clay is a good example of  plastic behavior.

But, few biological tissues obey Hooke’s Law, they actually behave as viscoelastic (a.k.a. viscoplastic) solids. There are two basic properties that describe their behavior: strength and stiffness. Cancellous bone is a viscoplastic biological structure. When cancellous bone is loaded quickly, it behaves as a fairly stiff material, it is resistant to deformation AND it tends to support higher loads. When cancellous bone is loaded slowly, it behaves as a less stiff material. “Visco” because cancellous bone deforms as a function of time. “Plastic” because once it deforms, cancellous bone doesn’t recover much, if any, of its original shape.

Final Thoughts

This is a very brief “taste” of biomechanical engineering as it relates to the properties and behavior of orthopaedic tissues. A more detailed discussion would include advanced testing techniques such as impact and fatigue testing, properties like ductility and toughness, and influences from age, gender, and disease.

Copyright (c) 2005      Susan G. Capps, Ph.D.